Binary Search Tree

Introduction

#

Definition A binary search tree is a binary tree whose left node (and its subelements) is smaller than the root and the right node (and its subelements) is greater than the root

Examples Adapted from GeeksForGeeks

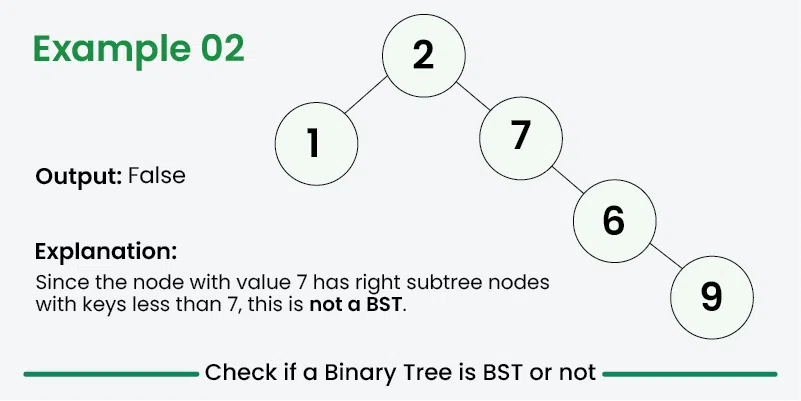
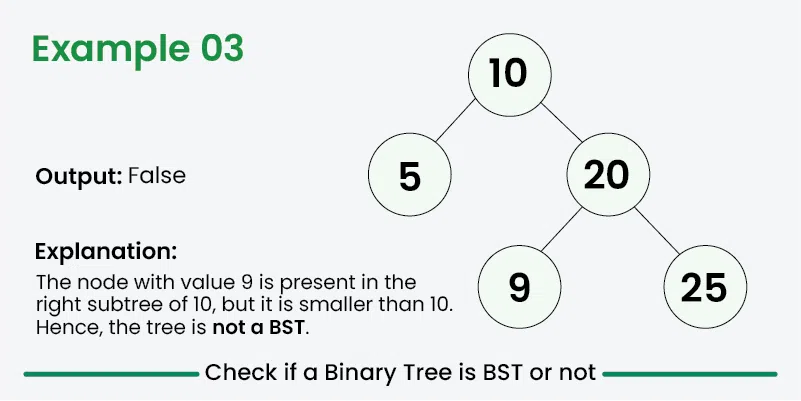
Application

#

Advantages

• Takes O(log n) time complexity searching for an element (in best cases)
• Items are sorted in a binary search tree, thus easier to find the adjacent elements to an element
• Insertions and deletions may be carried out efficiently
• Balanced BST maintains a logarithm height, thus ensuring efficient operations
• Both maximum and minimum may be maintained efficiently

Disadvantages

• Unbalanced BSTs lead to poor performance
• For searching and insertion, in worst cases, linear time complexity may occur
• It introduces more memory overheads
• BSTs can be inefficient for very large data sets
• BSTs only supports search, insertion and deletion - limited operations

Operations

#

Basics presenting the codes

#

/* For each node */
typedef struct node_t {
    node_t *left;
    node_t *rght;
    int val; // Here the value may be polymorphic
}

/* A helper linked list node for stack operations */
typedef struct link_t {
    node_t *node;
    link_t *next;
} link_t;

/* A helper linked list for stack operations */
typedef struct list_t {
    link_t *head;
    link_t *tail;
    int len;
}

/* Get new nodes by value */
node_t *new_node(int val)
{
    node_t *new = (node_t*)malloc(sizeof(node_t));
    new->left = NULL;
    new->rght = NULL;
    new->val = val;
    return val;
}

/* Return if is leaf node */
int isleaf(node_t *n)
{
    return n->left == NULL && n->rght == NULL;
}

/* Below are helper functions for linked lists */

/* Get an empty linked list node */
link_t *new_link(void)
{
    link_t *new = (link_t*)malloc(sizeof(link_t));
    new->node = NULL;
    new->next = NULL;
    return new;
}

/* Get an empty linked list */
list_t *new_list(void)
{
    list_t *new = (list_t*)malloc(sizeof(list_t));
    new->len = 0;
    new->head = NULL;
    new->tail = NULL;
    return new;
}

/* Insert a new node at the tail position, for queue */
void insert_tail(list_t *list, node_t *node)
{
    link_t *new = new_link();
    new->node = node;
    if(list->tail == NULL)
    {
        list->head = new;
        list->tail = new;
    }
    else
    {
        list->tail->next = new;
        list->tail = new;
    }
    list->len += 1;
}

/* Insert a new node at the head position, for stack */
void insert_head(list_t *list, node_t *node)
{
    link_t *new = new_link();
    new->node = node;
    if(list->tail == NULL)
    {
        list->head = new;
        list->tail = new;
    }
    else
    {
        new->next = list->head;
        list->head = new;
    }
    list->len += 1;
}

/* Extract a node at the head position */
node_t *pop_head(list_t *list)
{
    if(list->len == 0)
    {
        return NULL;
    }

    node_t *res = list->head->node;
    if(list->len == 1)
    {
        link_t *tmp = list->head;
        list->head = NULL;
        list->tail = NULL;
        free(tmp);
    }
    else
    {
        link_t *tmp = list->head;
        list->head = tmp->next;
        free(tmp);
    }
    list->len -= 1;

    return res;
}

Insertion

#

Basics

#

Process

• Compare the current node with the value to be inserted
• If the current node is leaf node
  • If the value to be inserted is greater, put the value on the right
  • Otherwise on the left
• If the current node is not leaf node
  • If the value to be inserted is greater, go through the comparison process with the node on the right
  • Otherwise with the node on the left

This process may be done by both recursively or iteratively

Time Complexity: $O(h)$ in the worst case where $h$ is the height of the binary search tree. If the tree degenerates to a singular linked list, it becomes $O(n)$

Space Complexity: $O(h)$ for recursive approach for calling stack, and $O(1)$ for iterative approach

Implementation

#

Recursive

void insert(node_t *head, int val)
{
    if(head->val > val)
    {
        /* In case we look at the right */
        if(isleaf(head))
        {
            /* If is leaf node, we insert */
            head->rght = new_node(val);
        }
        else
        {
            /* Otherwise we go through an other insertion comparison process */
            insert(head->rght, val);
        }
    }
    else 
    {   
        /* Otherwise we look at the left */
        if(isleaf(head))
        {
            /* Same analogy applies */
            head->left = new_node(val);
        }
        else
        {
            insert(head->left, val);
        }
    }
}

Iterative

void insert(node_t *head, int val)
{
    /* We keep track of the current node we are looking at */
    node_t *curr = head;
    do
    {
        if(curr->val > val)
        {
            if(isleaf(curr))
            {
                curr->rght = new_node(val);
            }
            curr = curr->rght;
        }
        else
        {
            if(isleaf(curr))
            {
                curr->left = new_node(val);
            }
            curr = curr->left;
        }
    } while (!isleaf(curr));
}

Search

#

Basics

#

As the name suggests, this kind of tree was first designed to carry out a binary search process

Process

• Compare the current value with the value on the node to see if they are equal
  • If so, then return true
  • If false, then see if the value can exist
• If the value is smaller than the node value
  • If the node has no left node, then return false
  • If there is, then do the search with the left node
• If the value is greater than the node value
  • If the node has no right node, then return false
  • If there is, then do the rearch with the right node

This process may be done by both recursively or iteratively

Time complexity & Space complexity: Same as insertion as the same analogy applies

Implementation

#

Recursive

int search(node_t *head, int val)
{
    if(head->val == val)
    {
        return 1;
    }

    if(head->val < val)
    {
        if(head->rght == NULL)
        {
            return 0;
        }
        return search(head->rght, val);
    }
    else
    {
        if(head->left == NULL)
        {
            return 0;
        }
        return search(head->left, val);
    }
}

Iterative

int search(node_t *head, int val)
{
    node_t *curr = head;
    if(curr->val == val)
    {
        return 1;
    }

    if(curr->val < val)
    {
        if(curr->rght == NULL)
        {
            return 0;
        }
        curr = curr->rght;
    }
    else
    {
        if(curr->left == NULL)
        {
            return 0;
        }
        curr = curr->left;
    }
}

Deletion

#

Basics

#

Process - Leaf nodes

• Free up the node to be deleted
• Set it to NULL on its precedecor

Process - With One Child

• Copy the pointer of its child and store temporarily
• Assign the properties of its child - i.e. left, right and value - to itself
• Free up the memory taken by its child

Process - With Two Children

• Find the inorder successor - i.e., the smallest element on its right branch - by using recursive or iterative approach
• Swap the values of its inorder successor with the current node
• Delete its inorder successor - An inorder successor will be a leaf node or has only one right child, or it will not be an inorder successor

Implementation

#

Too long to write them all, so good reference material provided below More to explain

Depth First Search

#

Basics

#

Depth First Search is based solely on one thing - the stack. You first track the child, then the parent - this is essentially what is meant by stack - you track what is been input last, then what is been input first

All depth first traversal follow the same order visiting the nodes - it is just that the juncture visiting the nodes differs

There are three types of traversals categorized under depth first search, namely - Pre-order, in-order and post-order - by visiting the node before, at and after traversing it

Without considering visiting the nodes, i.e. only to record the sequence first reaching nodes, we may use both recursive and iterative approach

Here for simplicity, we only consider depth-first searching binary trees - for higher ranked binary trees we only need to modify the framework a little bit

Recursive:

void depth_first_search(node_t *n)
{
    /* First, we record where we are, suggesting our first visit to this node */
    fprintf(stdout, "%d\n", n->val);

    /* Then, we look at our left, and right */
    depth_first_search(n->left);
    depth_first_search(n->rght);
    
    return;
}

To build up an iterative approach from a recursive function, what we need to keep in mind is that the function stack did the stack work we are meant to do in an iterative approach

Speaking of a function stack, the later the function call is put in the stack, the earlier the function call is processed - i.e. we need to implement our own stack, that simulates a function call

• We call our own function first - i.e. print the value first
• Then we put the next calls accordingly - in this case, though, the original function calls left first - But we need to put the right call first so as to guarantee that the left call is, in practice, initiated first

Then we try to do what we aimed to do

Iterative

void depth_first_search(node_t *n)
{
    list_t *stack = new_list();
    insert_head(stack, n);

    while(stack->len != 0)
    {
        node_t *curr = pop_head(stack);
        
        /* Complete the "function call" */
        fprintf(stdout, "%d\n", curr->val);

        /* Insert more elements into the stack accordingly, 
        first right then left, so that it searches left first then right */
        if(curr->left != NULL)
        {
            insert_head(stack, curr->left);
        }
        if(curr->rght != NULL)
        {
            insert_head(stack, curr->rght);
        }
    }
}

Also, this is identical to pre-order traversal

Pre-order Traversal

#

Essentially the basic version of depth-first search

Time Complexity: $O(n)$

Space Complexity: $O(h)$ because of the stack

In-order Traversal

#

In-order traversals are especially helpful in BSTs, as it is guaranteed to track all values in ascending order

For each in-order traversal, it is guaranteed that